Keď som si pred pár rokmi pripravovala prednášku o násobení, narazila som v knihe od profesora Čižmára – História matematiky na zaujímavú pasáž – násobenie v starovekom Egypte. V tom čase totiž nemohli násobiť tak, ako to robíme dnes. Nepoznali pozičný spôsob zápisu čísel. Čísla zapisovali pomocou niekoľkých znakov. Mali znak pre jednotku, desiatku, stovku, tisícku a t.ď. Všetky ostatné čísla zapísali hromadením týchto znakov. Čiže dvadsať päť napísali ako dva znaky desiatky a päť znakov jednotky. Takto zapísané čísla by sa naším známym algoritmom násobili pomerne ťažko. Oni používali efektívnu metódu, ktorá sa, mimochodom, dá rovnako dobre používať aj dnes.

Keď som o násobení zdvojovaním čítala prvý krát, tak veľmi ma to nadchlo, že som naprogramovala aj jednoduchú aplikáciu, ktorá užívateľa naučí, ako sa to robí. Zverejnila som ju na google play pod názvom Egyptské násobenie a delenie. Skoro nikto si ju nestiahol. Chcela som sem pridať obrázok, ako vyzerala, ale už ju neviem nájsť. Asi mi ju vymazali. 😕
Princíp je založený na fakte, že násobenie je iba opakované sčítavanie. Unikátna je metóda, ako toto sčítavanie zrýchliť zmenšením počtu sčítancov. Napríklad pri násobení 17tkou netreba sčítať 17 rovnakých sčítancov, ale oveľa menej. V tomto konkrétnom príklade by to boli iba dva. Ako je to možné? Odpoveďou je opakované zdvojnásobovanie.
Príklad: 17×25. 25 idem opakovane zdvojnásobovať. Dvojnásobok 25ky je 50, dvojnásobok 50tky je 100, dvojnásobok stovky je 200 a t.ď. Vtip je v tom, že toto si píšem pod seba a do príslušného riadku vždy píšem aj koľko násobok pôvodnej 25ky to je. Pri 50 mám dvojku, pri 100 štvorku, pri 200 osmičku.
1, 2, 4, 8, 16, 32, … to je postupnosť mocnín dvojky. A z týchto čísel treba zložiť druhého činiteľa, t.j. v tomto príklade 17ku. 17=16+1 takže si vyznačím riadky, v ktorých je 16 a prvý, kde mám 1 – to je ten prvý s 25kou. No a keď sčítam šestnásťnásobok 25ky s jednonásobkom, tak, pochopiteľne, dostanem sedemnásťnásobok. Takto by to vyzeralo:
1……25
2……50
4…..100
8…..200
16…400
400+25=425
V poriadku, poviete si, ale pre veľké čísla to bude určite neskutočne zdĺhavé. Ale nie je to tak. Tu sa ukáže krása mocnín. Rastú totiž najprv nepatrne, ale neskôr sa vám zatočí hlava z toho prudkého rastu. Pri sedemnástke sme potrebovali päť riadkov. Koľko riadkov by bolo potrebných pre desaťmiestne čísla?
2 na 33 je niečo vyše 8,5 miliardy, takže pri egyptskom násobení čísel menších ako desať miliárd nám vystačí pokojne 33 riadkov. Jedna A4.
Príklad
Tak to sa musí vyskúšať. Už ste sa niekedy zamýšľali nad tým, koľko je 123456789 x 987654321? Nie? Kalkulačka veľmi nepomôže – je to priveľa, výsledok len zaokrúhli. Tak som dnes vo chvíľkach, ktoré sa mi podarilo ukradnúť si pre seba, násobila po egyptsky. Trvalo to asi pol hodinku. A potom ešte tri hodiny, kým som našla a opravila všetky chyby. 😁
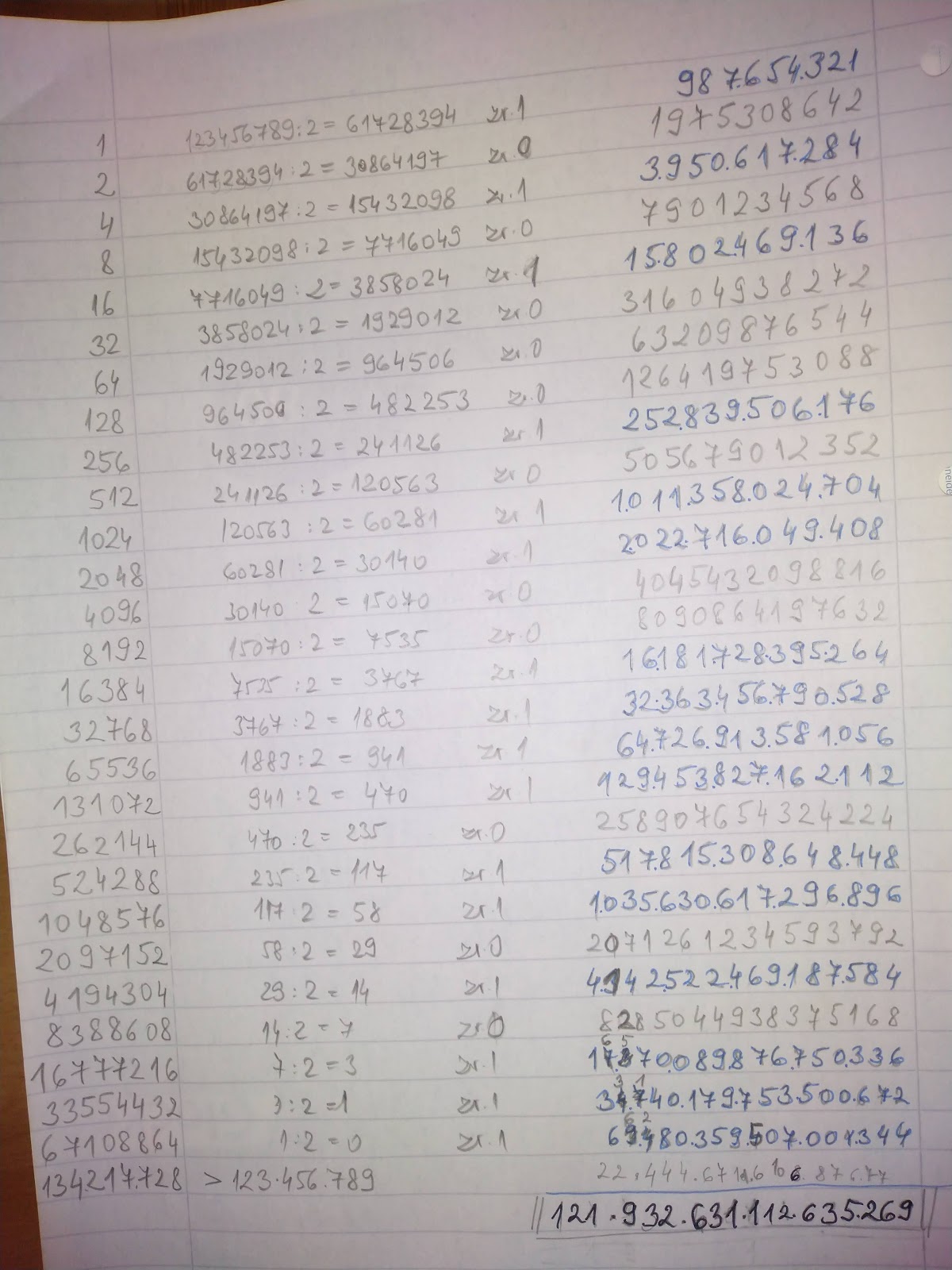
Ak vás zaujíma, čo som to tam porobila, za chvíľu vysvetlím. Ak nie, tak tu môžete skončiť a prípadne sa pobaviť pri násobení maličkých čísel. Napríklad 36 x 63, výsledok si ľahko overíte na kalkulačke. Moja rada: zdvojnásobujte to väčšie číslo a to menšie potom vyskladajte z mocnín dvojky. Alebo aj nie. Niekedy to môže byť aj dlhšie ako naopak. Napríklad 63 x 71 bude o dosť rýchlejšie, ak si vyskladáte 71tku…
Pre tých, ktorí majú podobnú predstavu o zábave ako ja, prikladám pár postrehov. Stĺpec úplne vľavo obsahuje mocniny dvojky. Úplne vpravo zasa dvojnásobky čísla 987654321. V strede mi zostalo dosť miesta, tak som tam umiestnila výpočet, ktorým som určila, ktoré riadky budem potrebovať. Mohla som to, samozrejme, spraviť aj klasicky – pozriem najvyššiu mocninu menšiu ako 123456789, označím ten riadok a zistím rozdiel. K nemu zasa nájdem najvyššiu mocninu menšiu od neho a t.ď. To sa mi ale nechcelo, tak som použila algoritmus, ktorým sa prevádza číslo do dvojkovej sústavy. Je dosť ľahký: iba delíte dvojkou a zapisujete zvyšky. Ja som si to tak pekne rozmiestnila, že tam, kde mám zvyšok jeden, to je práve ten riadok, ktorý potrebujem označiť. Takže v riadkoch s jednotkou som vpravo obtiahla čísla a tie som následne sčítala. To je všetko. Brnkačka.
Skúška správnosti
Až na to, že som, ako vždy, porobila pár numerických chýb, ktoré treba nájsť a opraviť. Ako som vedela, že mám zlý výsledok? Tak po prvé, už sa poznám. A po druhé nesedí deviatková skúška.
Deviatková skúška je úplne nádherná vec. Nechápem, že sa o nej skoro nikde neučí. Ja som na ňu narazila v podstate náhodou. Ide o to, že keď používate iba súčet, rozdiel a súčin a máte veľké čísla, zredukujete celé zadanie na zvyšky po delení deviatkou. Zvyšok po delení deviatkou sa totiž nájde veľmi ľahko – stačí určiť zvyšok ciferného súčtu. V mojom prípade 1+2+3+4+5+6+7+8+9. Druhý činiteľ má ciferný súčet úplne rovnaký, všakže. Ja som tak lenivá, že ani toto nesčítavam. Čísla zoskupujem do deviatok a tie vyhadzujem, až mi niečo zostane. Tu mám 9, potom 1+8, 2+7, 3+6, 4+5. Nič nezostalo, číslo je teda deliteľné deviatkou bezo zvyšku. No a keď vynásobíme dve čísla deliteľné deviatkou, tak aj výsledok musí byt deliteľný deviatkou. Ak nie je, niekde je zaručene chyba. Ak je, stále tam niekde môže byť chyba, ale je to málo pravdepodobné.
Ešte poznámka k deviatkovej skúške – ak by tam nejaké zvyšky vyšli, treba urobiť všetky operácie s týmito zvyškami a aký zvyšok bude mať výsledok, taký zvyšok musí mať aj celý vypočítaný výsledok. Čiže, ak by sme násobili čísla, z ktorých jedno dáva zvyšok 4 a druhé 7, ich súčin je 28, čo je zvyšok 1. A teda celkový výsledok musí mať zvyšok 1. Elegantné a rýchle. 😍
No, ale mne deviatková skúška nevyšla, takže som musela pátrať. A tu prinášam ešte dva spôsoby overenia:
Kontrola spredu spočíva v tom, že čísla normálne vynásobím na kalkulačke. Ona sice výsledok zaokrúhli, ale prvých niekoľko cifier bude správnych. Stačí porovnať.
Kontrola odzadu je taká menej známa finta. Ak totiž vynásobíte len niekoľko posledných cifier, toľko isto cifier odzadu bude správnych. Mne kalkulačka zvládla násobiť bez zaokrúhľovania päťciferné čísla. Tak som násobila 56789 x 54321. Posledných päť cifier výsledku je správnych. Túto kontrolu používam na poslednú jednu cifru dosť často. 😉
Po týchto kontrolách zostali len tri až štyri miesta, kde ešte mohla zostať chyba. Zákon schválnosti opäť funguje, pretože práve tam bola. 😏
Takže 123.456.789 x 987.654.321 = 121.932.631.112.635.269, také pekné zadanie a tak nezaujímavý výsledok. 🤣
